代ゼミ教育総研

数学講師　　大山　壇

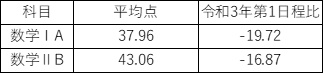
― 令和4年の共通テストでは、数学ⅠAと数学ⅡBどちらも平均点が低下しています。
　特に数学ⅠAは過去に例がないほど平均点が低かったということでメディアでも取り上げられました。
　なぜ、ここまで平均点が低下してしまったのでしょうか。
　

数学ⅠAの受験生は35万７千人で数学の苦手な生徒も受験する科目です。例年であれば、そうした生徒も〈数と式〉や〈２次関数〉である程度の点数を取ることができたのですが、令和4年の数学ⅠAでは、これらの分野についても比較的難しめの問題が出題されました。第1問[1]〈数と式〉は、3文字の対称式に関する問題でしたが、センター試験の対称式は原則として2文字での出題でしたから戸惑った受験生もいたと思います。第2問[1]〈2次関数/集合と命題〉は、2次方程式の解の配置をグラフ化して考える問題でしたが、誘導が十分ではありませんでした。数学が得意でない受験生は問の意図を把握できず、苦戦してしまったでしょう。
また、数学ⅠAでは非常に厳しい計算が課されたことも点数低下の要因と考えられます。第1問[2]〈図形と計量〉の三角比に関する問いでは、0.2867÷4という計算を行う必要があります。従来のセンター試験ではここまで細かい計算問題は見られませんでした。第2問[2]〈データの分析〉で相関係数を求める問題にも、735.3÷（39.3×29.9）という計算が登場します。こちらも以前のセンター試験であれば、選択肢から近い値を選べという形で問われていました。更に、第4問〈整数の性質〉では5桁の数値を求める計算を2回も行わなくてはなりません。

― では、数学ⅡBについてはどうだったのでしょうか。

やはり1問1問がある程度難しく、それでいて各問題の分量が多かったことが一番の要因だと思います。どの問題も個別入試対策に使えるようなじっくりと考えさせる良問ぞろいでしたが、試験時間とボリュームがつり合っていないというのが私の印象です。私の見立てでは、数学ⅡBと数学ⅠAどちらも試験時間が90分であれば、平均点が50点台に届いたのではないかと思います。
例えば、第4問〈数列〉では、非常に長いリード文による詳細な説明を用いて「規則的な変化を示すグラフと数列の対応」について考えさせる場面を設定しています。こうした考え方は大学や企業における数理的な実験ではよくあるものですので、高校での学習内容を実社会における活用例にあてはめる問題を目指したのではないでしょうか。意欲的な出題でしたが、単独で良い問題かどうかと試験問題の一つとして適正かどうかは分けて考える必要があります。10分から15分で正解しなくてはいけないと考えるとこの問題については、受験生への負担が大きすぎたと思います。
また、第1問[2]〈指数関数・対数関数〉では、logに関する問題が出題されています。この問題だけで4ページもあり、例年の第1問と比べるとかなり長くなっています。似たような内容は過去に何度も問われているのですが、共通テストでは抽象度を高めるために文字を使ったことでより複雑な問題になりました。大学入試センターとしては、抽象度を高めた問題を出題することで、学校教育における思考力の育成を促したいのだと思いますが、個人的には抽象度を高めるだけでは、思考力にはつながらないと考えています。

― では、どのような問題であれば思考力を高めることができるのでしょうか。

例えば文字式の場合分けなどについて、生徒自身が「場合分けが必要なのか」、「どのように場合分けするのか」を考えて判断できることが本当の意味での思考力だと思います。仮に文字の数が一つであったとしても、それをもとに生徒自身が試行錯誤できる余地があれば思考力を測ることができます。センター試験ではそうした問題が出題されていました。令和4年共通テストの問題はどれも複雑ですが、場合分けの条件などについては、問題文中に明記されていますから、生徒が考える必要はありません。長文化や複雑化の背景には、必要な情報を見つけ出し解答方針を受験生に定めさせるという目標があったはずですが、誘導によって方針は一つに定まってしまっています。
特に数学ⅡBでそうした傾向が顕著ですが、思考要素を盛り込もうとした結果として複雑さが増したことで、思考力ではなく処理力が点数につながる試験になってしまいました。例えば第1問[1]〈図形と方程式/三角関数〉では、接線を求めるためには「二次方程式に代入する」、「タンジェントを用いる」という二つのアプローチが考えられるのですが、どちらも問題文中に明記してしまっています。本来こうしたアプローチの方針を検討することこそ思考のはずです。実はこの問題には、点と直線の距離の公式を用いるというメジャーな解法もあります。それをあえて外した点は良いのですが、残りの解法を全て示してしまったことで結果的に受験生の思考を促すことは出来ませんでした。
実は問題というものは、長くなるほど様々な条件から解答方針が自然と一つに定まってしまうのです。東大の「円周率が3.05より大きいことを示せ」や京大の「tan1°は有理数か否か」のようにどこから手をつければ良いか一見すると分からない問題こそが、本当の意味で考えさせる問題なのです。

― 複数の要因があって難化したのですね。令和5年の共通テストでもこの難易度が維持されるのでしょうか。

いくらなんでも令和4年試験の平均点は低くなりすぎですから、多少の揺り戻しはあると思います。平均点が50点～60点程度であれば、偏差値が50に届かない受験生の点数にもある程度の階層が生じるので、数学が苦手な受験生でも努力が結果の差につながりますが、令和4年数学ⅠAのように平均点が30点台では、数学が苦手な受験生の点数にはほとんど差がなかったでしょう。成績分布が非常に密になってしまった影響でデータリサーチの判定もわずかな点差で覆ってしまいます。実際はB判定とD判定で大きな点数差がないケースであれば、二次試験での挽回も期待できるのですが、判定の悪かった受験生の中には志望校を諦めてしまった人もいました。令和4年に関しては、上位の大学では実質的に二次試験だけでの勝負になりかねません。こうした状況では一次試験として共通テストを行う意義が薄れてしまいます。
ここまで数学で点数が取りにくい状況が続いてしまうのであれば、数学の勉強量が点数に結びつかず、他の受験生に対する優位につながらないため、より点数の取りやすい教科に力を入れようと考える受験生が増え、結果的に理系離れや国立離れが進んでしまうことが危惧されます。そうした点からも令和５年は易しくする方向への調整が行われるでしょう。ただし、多くの意図を盛り込み作問した大学入試センターの決意は固いと思われ、出題方針そのものは維持されると予想されます。

― 今後の共通テストに向けてどのような指導を行うべきでしょうか。

まず、「センター試験であれば、典型問題を覚えて試験では目先の空欄を一つ一つ何とか埋めていくという姿勢でもある程度の点数を取ることができたが、共通テストではそうした方法は一切通用しない」ということを生徒たちにはっきりと伝える必要があります。令和４年の出題方針が維持されるのであれば、共通テストでは、「長い問題文の題意を短時間で把握し、それらを図やグラフに落とし込み、そこから必要な情報を拾い出して、導き出された計算式を正確に処理する」能力が求められます。共通テストの問題そのものは非常に良い教材としてのポテンシャルを秘めていますが、それらを時間内に解くことを意識した勉強は、学校での教科書を使った勉強とも二次試験に向けた勉強とも乖離していますから、共通テストに特化した対策が欠かせません。
共通テストの数学を受験する生徒であれば、仮に二次試験や個別入試で数学が必要ない場合でも、「一から自分で考える必要のある二次試験型の頭の使い方を身につけさせること」が重要です。また、「会話文や長いリード文から情報を見つけ出す練習」をさせた方が良いですから、過去問、予想問題集や模試も活用してください。当面はこの二つが対策の二本柱になるでしょう。